Способы решения логических задач.Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач: Познакомимся с ними поочередно. I. Решение логических задач средствами алгебры логикиТ.е. с помощью составления логической формулы, упращения её с помощью законов логики и доказательства её истинности при каких-то значениях исходных логических высказываний.
Задача:На вопрос, какая завтра погода, синоптик ответил: если не будет ветра, то будет пасмурная погода без дождя; если будет дождь, то будет пасмурно и без ветра; если будет пасмурно, то будет дождь и не будет ветра. Подумав немного, синоптик уточнил, что его три высказывания можно записать более лаконично. Попробуйте это сделать!Решение:Обозначим буквой В - высказывание: 'будет ветер'Буквой Д - высказывание: 'будет дождь' Буквой П - высказывание: 'будет пасмурно' По высказываниям синоптика составляем формулы: 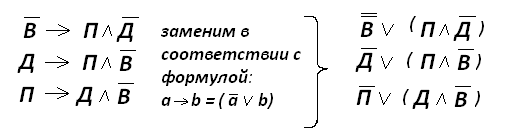
Так как все эти высказывания истинны, то их конъюнкция так же должна быть истинна: 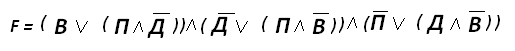
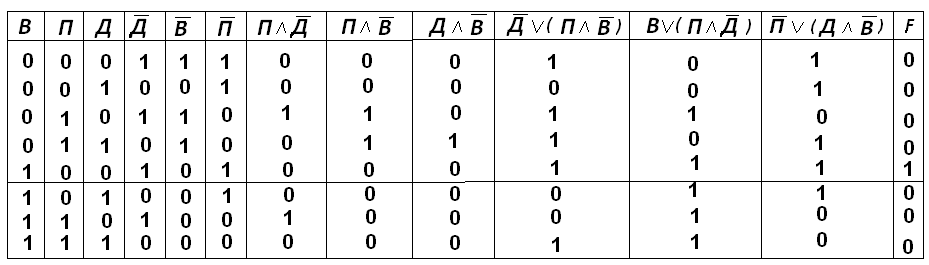
Составив таблицу истинности полученной функции, выявляем, что она истинна только в единстенном случае, при В=1, Д=0, П=0.
Ответ:Завтра если будет ветер, то будет ясно и не будет дождя.II. Решение логических задач табличным способомПри использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц. 
По условию задачи нарисуем таблицу, в которой названия столбцов - имена собак, а названия строк - цвета ошейников: 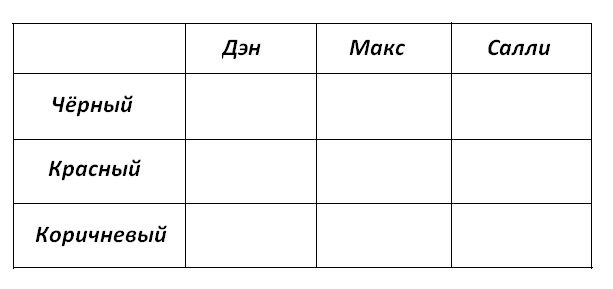
Рассуждая по условию задачи, заполняем таблицу минусами и плюсами: т.к. глаза собаки не могут быть красными, то ставим в таблицу минус в ячейку Дэн-Красный. Сын Салли может быть только Макс, т.к. Дэн всех старше, поэтому ставим плюс в ячейку Макс-чёрный и заносим минусы во все ячейки столбца и строки, на пересечении которых поставлен плюс. Тогда в столбце Дэн остаётся место для плюса только в строке Коричневый и у Салли ставим плюс в строке Красный. Получается таблица вида: 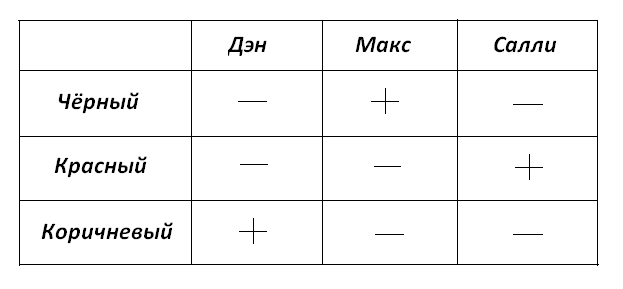
Ответ: У Дэна коричневый ошейник, у Макса - чёрный, а у Салли - красный. 
III. Решение логических задач с помощью рассужденийЭтим способом обычно решают несложные логические задачи.
Задача:Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?Решение:Имеется три утверждения:
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это тоже противоречит условию задачи о том, что кто-то из ребят изучает китайский язык, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей. Ответ:Сергей изучает китайский язык, Михаил — японский, Вадим — арабский. |