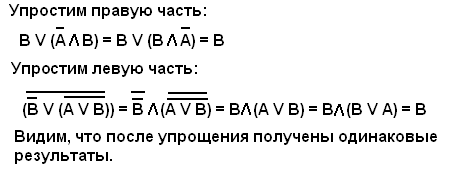Mатематическая логика. Тест.Задачи.Математическая логика– это область знаний, которая изучает истинность или ложность высказываний.Утверждения в математической логике называются логическими выражениями. Заметим. Что любое высказывание или логическое выражение не может быть одновременно истинным и ложным, а принимает только одно из этих двух возможных логических значений: ИСТИНА или ЛОЖЬ. Эти значения называются в математической логике логическими постоянными, или логическими константами. Связки в сложных высказываниях:'И', 'ИЛИ', 'НЕ'... в математической логике называют операциями. Иначе математическую логику называют символьной логикой. Все высказывания в ней записываются с помощью букв, а операции - с помощью специальных символов. Различают следущие операции математической логики:
Познакомимся с ними поочередно, с порядком их выполнения и законами математической логики. I. Логическое сложение (дизъюнкция).Объединение простых высказываний связкой ИЛИ, называют логическим сложением или дизъюнкцией. Обозначают: 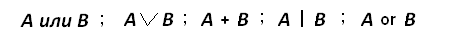
Для определения истинности или ложности результатов логических операций пользуются таблицами истинности, где ИСТИНА и ЛОЖЬ обозначаются 1 и 0. Для логического сложения таблица истинности выглядит так: 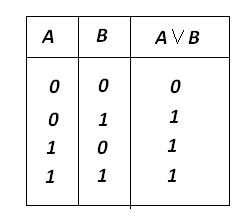
II. Логическое умножение (конъюнкция).Объединение простых высказываний союзом И, называют логическим умножением или конъюнкцией.Обозначают: 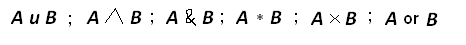
Для логического умножения таблица истинности выглядит так: 
III. Логическое отрицание (инверсия).Присоединение частицы НЕ к сказуемому данного простого высказывания, называют логическим отрицанием или инверсией. Обозначают: 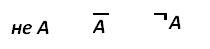
Для логического отрицания таблица истинности выглядит так: 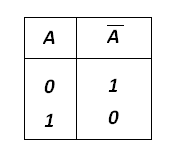
IV. Логическое следование (импликация).Сложное логическое высказывание , образованное с помощью связки 'ЕСЛИ..., ТО...' называют логическим следованием или импликацией. Обозначают: Для логического следования таблица истинности выглядит так: 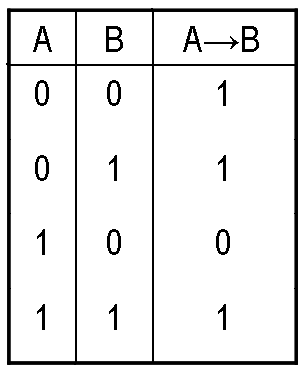
V. Логическое равенство (эквивалентность).Сложное логическое высказывание , образованное с помощью связки 'ТОГДА И ТОЛЬКО ТОГДА...' называют логическим равенством или эквивалентностью. Равнозначность называют также эквиваленцией. Обозначают: Для логического равенства таблица истинности выглядит так: 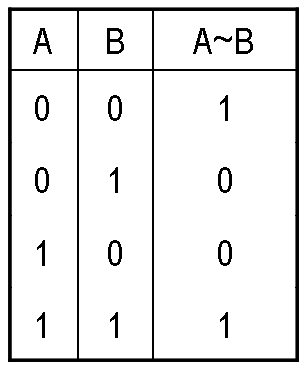
Порядок выпролнения логических операций.Для логических операций порядок выполнения в заданной логической функции (составного высказывания) выглядит так: 
Законы математической логики.Так же как в математике в логике существуют формулы, которые позволяют преобразовывать логические выражения. Некоторые из них очевидны, другие доказываются путём построения таблиц истинности для левой и правой частей формулы и последующим их сравнением. Познакомимся с наиболее популярными из формул: 

Виды задач по математической логике.Задача 1. Составьте таблицу истинности для заданной функции: 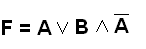
Решение: Составим таблицу истинности для всех возможных значений высказываний, входящих в заданную функцию. Количество всех возможных значений определяется по формуле: 2n, где n - количество входящих в функцию высказываний. Т.к. у нас в функцию входит только 2 высказывания - А и В, то возможных значений будет 22 = 4. Упрощаем работу, находя значения истинности функции по действиям. Порядок действий при этом надо соблюдать! Он как в математике: 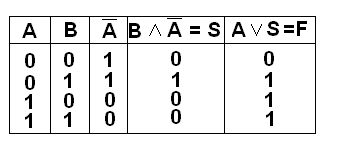
Задача 2. Докажите равенство логических выражений с помощью таблиц истинности: 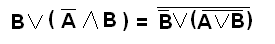
Решение: Составим таблицу истинности для обеих частей равенства, как в 1 задаче: 
Сравним результаты в последних колонках. Если результаты совпали, то и функции равны. Ответ:функции равны RS. Проще доказать равенство этих функций было бы с помощью законов математической логики::
Задача 3. Определите при каких значениях выражений заданная функция ложна: 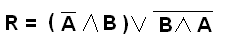
Решение: 1 способ: Составим полную таблицу истинности функции, как в 1 задаче: 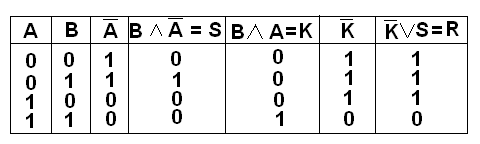
Выберим строку с исходными значениями входящих в функцию выражений, при которых значение последний колонки - 0: 2 способ: Заданная функция ложна только тогда, когда оба слогаемых ложны. Слогаемое ¬ (A /\ B) - ложно, если (A /\ B) - истинно. Произведение истинно, если оба сомножителя истинны, т. е. А=1 и В=1. Ответ: при A=1 , B=1 Задача 4. Докажите равенство логических выражений с помощью законов математической логики: 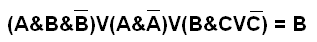
Решение: Упращаем левое логическое выражение, пользуясь законами математической логики: непротиворечия и исключённого третьего 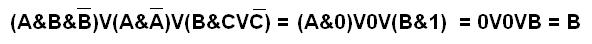
В результате пришли к виду правого логического выражения. Ответ: логические выражения равны. |